Как рассчитать сердечник и витки самодельных катушек индуктивности

Расчет сечения кабеля по мощности и длине + ТАБЛИЦА

Калькулятор расчета сечения кабеля по мощности и току поможет вам рассчитать сечение кабеля, минимально необходимое для безопасной эксплуатации электропроводки, чтобы избежать перегревов, плавления изоляции, короткого замыкания и пожаров.

Калькулятор позволяет производить расчет сечение кабеля по току или мощности, исходя из параметров общей нагрузки и поступающего напряжения. При этом учитываются условия прокладки, материалы изготовления проводов, возможные потери напряжения и критерии выбора проводника. Функционал раздела позволяет также произвести расчет максимального тока и нагрузки на проводник с заданными параметрами и выбрать устройства защиты (автоматические выключатели, дифференциальные автоматы и УЗО).

Как производится расчет сечения кабеля:

1. Укажите исходные данные (ток или мощность), напряжение, материал изготовления проводника (медь или алюминий), тип проводки (открытую или закрытую в трубе), количество проводов (при прокладке коммуникации в трубе);
2. Отметьте дополнительные условия (длину провода, допустимые потери);
3. Нажмите на кнопку «Рассчитать» и сохраните полученные параметры.

Калькулятор расчета сечения кабеля работает в онлайн и в офлайн режиме

Обратите внимание: он носит исключительно рекомендательный характер и не может гарантировать 100% верность подсчетов. Однако чем больше достоверных данных вы введете в соответствующие поля, тем выше будет процент соответствия

Смежные нормативные документы:

1. ПУЭ-7 «Правила устройства электроустановок»
2. СП 76.13330.2016 «Электротехнические устройства»
3. ГОСТ Р 50571.5.52-2011/МЭК 60364-5-52:2009 «Электроустановки низковольтные. Выбор и монтаж электрооборудования»
4. ГОСТ 31946-2012 «Провода самонесущие изолированные и защищенные для воздушных линий электропередачи»
5. ГОСТ 31947-2012 «Провода и кабели для электрических установок на номинальное напряжение до 450/750 В»
6. ГОСТ 6323-79 «Провода с поливинилхлоридной изоляцией для электрических установок»
7. ГОСТ 31996-2012 «Кабели силовые с пластмассовой изоляцией на номинальное напряжение 0,66; 1 и 3 кВ»
8. ГОСТ 433-73 «Кабели силовые с резиновой изоляцией»

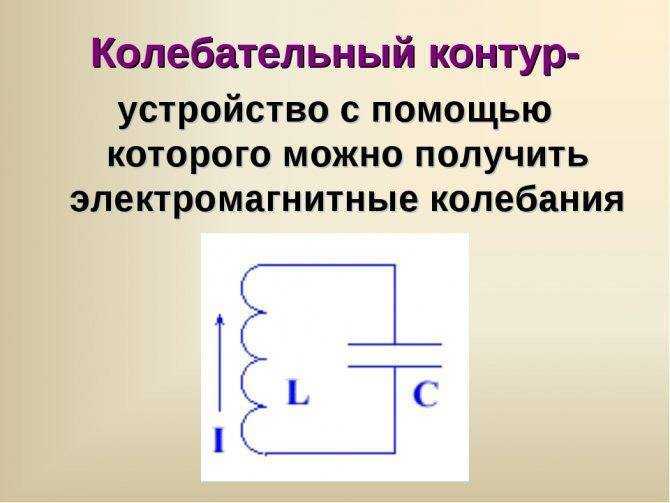
Что такое катушка индуктивности

Данный элемент ещё называют дросселем. Это свёрнутый в спираль изолированный провод. Для такой спирали характерны большие индуктивные и маленькие ёмкостные параметры.

Важно! Дроссель препятствует протеканию переменного тока, потому что обладает существенной инерционностью. Она препятствует любому изменению проходящего через витки тока. При этом нет разницы, увеличивается он или уменьшается

При этом нет разницы, увеличивается он или уменьшается.

В связи с этим данные элементы применяют в электротехнике для осуществления:

• токоограничения;
• ослабления биений;
• помехоподавления;
• формирования магнитного поля;
• изготовления датчиков движения.

Дроссель входит в систему колебательного контура в цепях резонанса и применяется в линиях задержки.

Расчет длин кабеля калькулятор

• Каталог
  • Назад
  • Каталог
  • Кабель силовой
  • Кабель управления и контроля
  • Кабель судовой
  • Кабель монтажный
  • Кабель передачи данных
  • Кабель греющий
  • Провода
  • Электротехнические товары
• Акции
• Инфо
  • Назад
  • Инфо
  • Статьи о кабеле
  • Вопрос-ответ по кабелю
  • Калькулятор веса кабеля
  • Калькулятор сечения кабеля
  • Производители кабеля
  • Партнерство
• Доставка и оплата
• О компании
  • Назад
  • О компании
  • Склады
  • Новости
  • Сотрудники
  • Сертификаты
  • Отзывы
  • Документы и реквизиты
  • Объекты наших клиентов
  • Вопросы по работе компании
• Контакты
  • Назад
  • Контакты
  • Филиалы

Санкт-Петербург, 196158, Московское шоссе, д. 42, корпус 2, лит. А, офис 315

ОБЩАЯ ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

Накопленная энергия в индуктивности Гидравлическая модель Индуктивность в электрических цепях Схемы соединения катушек индуктивностей Параллельное соединение индуктивностей Последовательное соединение индуктивностей Добротность катушки индуктивности Катушка индуктивности. Формула индуктивности Базовая формула индуктивности катушки Индуктивность прямого проводника Индуктивность катушки с воздушным сердечником Индуктивность многослойной катушки с воздушным сердечником Индуктивность плоской катушки Конструкция катушки индуктивности Применение катушек индуктивности Расчет катушек индуктивности Метод определения собственной ем­кости катушек Расчет и изготовление плоских катушек индуктивности

Катушка индуктивности

— является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.

Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.

Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.

Сопротивление индуктивное Википедия

Реакти́вное сопротивле́ние

(реактанс) — электрическое сопротивление, обусловленное передачей энергии переменным током электрическому или магнитному полю (и обратно).

Реактивное сопротивление определяет мнимую часть полного сопротивления (импеданса):

Z=R+jX{\displaystyle Z=R+jX}, где Z{\displaystyle Z} — полное сопротивление или импеданс, R{\displaystyle R} — величина активного сопротивления, X{\displaystyle X} — величина реактивного сопротивления, j{\displaystyle j} — мнимая единица.

В зависимости от знака величины X{\displaystyle X} какого-либо элемента электрической цепи говорят о трёх случаях:

• X>0{\displaystyle X>0} — элемент проявляет свойства индуктивности.
• X=0{\displaystyle X=0} — элемент имеет чисто активное сопротивление.
• X<0{\displaystyle X<0} — элемент проявляет ёмкостные свойства.

Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений:

X=XL−XC{\displaystyle X=X_{L}-X_{C}}

Индуктивное сопротивление

(XL{\displaystyle X_{L}}) обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи. Изменение тока и, как следствие, изменение его магнитного поля вызывает препятствующую изменению этого тока ЭДС самоиндукции. Величина индуктивного сопротивления зависит от индуктивности L{\displaystyle L} элемента и угловой частоты ω{\displaystyle \omega } протекающего тока: XL=ωL=2πfL{\displaystyle X_{L}=\omega L=2\pi fL}Ёмкостное сопротивление

(XC{\displaystyle X_{C}}). Величина ёмкостного сопротивления зависит от ёмкости элемента C{\displaystyle C} и также частоты протекающего тока f{\displaystyle f}: XC=1ωC=12πfC{\displaystyle X_{C}={\frac {1}{\omega C}}={\frac {1}{2\pi fC}}} Здесь ω{\displaystyle \omega } — циклическая частота, равная 2πf{\displaystyle 2\pi f}.

Расчет катушки Тесла

Без расчетов можно изготовить слишком большой трансформатор, но разряды искры сильно разогревают воздух, создают гром. Электрическое поле выводит из строя электрические приборы, поэтому трансформатор необходимо располагать подальше.

Для расчета длины дуги и мощности расстояние между проводами электродов в см делится на 4,25, далее производится в квадрат, получается мощность (Вт).

Для определения расстояния корень квадратный от мощности умножается на 4,25. Обмотка, создающая разряд дуги в 1,5 метра, должна получать мощность1246 ватт. Обмотка с питанием в 1 кВт создает искру в 1,37 м длины.

Схема замещения реальной катушки в с параллельным соединением элементов

Для реальной катушки можно составить и другую расчетную схему — с параллельным соединением двух ветвей: с активной G и индуктивной BL проводимостями. На рис. 13.12, б эта схема показана в сравнении со схемой последовательного соединения активного и индуктивного сопротивлений (рис. 13.12, а), рассмотренной ранее. Покажем, что схемы рис. 13.12, а, б эквивалентны в том смысле, что при одинаковом напряжении сохраняются неизменными ток в неразветвленной части цепи, активная и реактивная мощности.

Вектор тока I можно разложить на две взаимно перпендикулярные составляющие и в соответствии со схемой и векторной диаграммой на рис. 13.12, б выразить векторным равенством

                                             I = IG + IL                                           (13.24)

Для схемы параллельного соединения активного и индуктивного элементов общим является приложенное напряжение, а токи разные: IG —ток в ветви с активной проводимостью, по фазе совпадает с напряжением; IL — ток в ветви с индуктивной проводимостью, по фазе отстает от напряжения на угол 90°.

Вектор тока I и его составляющие IG и IL образуют прямоугольный треугольник, поэтому

Составляющая тока в активном элементе

IG = Icosφ

Проекция вектора тока I на направление напряжения называется активной составляющей вектора тока и обозначается Iа. Для катушки по схеме на рис. 13.12, б Ia = IG.

Составляющая тока в реактивном элементе

IL = Isinφ

Проекция вектора тока I на направление, перпендикулярное вектору напряжения, называется реактивной составляющей вектора тока и обозначается Iр. Для катушки Iр = IL .

Стороны треугольника токов, выраженные в единицах тока, можно разделить на напряжение U и получить подобный треугольник проводимостей, катетами которого являются активная G = IG/U и индуктивная ВL = IL/U проводимости, а гипотенузой — величина Y = I/U, называемая полной проводимостью цепи.

Из треугольника проводимостей и с учетом ранее полученных выражений из треугольника сопротивлений получим

Это интересно: Двигатель токарного станка не запускается, пускатель срабатывает — читаем во всех подробностях

Расчет параметров катушки

Приходится при расчётах рассматривать разные варианты. Расчет индуктивности зависит от исходных данных и заданных конечных параметров.

Расчет L в зависимости от заданной конструкции

Если исходными параметрами являются: w, D каркаса и длина намотанного провода, то формула для расчёта имеет вид:

L = 0,01*D*w2/(l/D) + 0,46,

где:

• D – диаметр каркаса, см;
• w – число витков;
• l – длина намотки, см;
• L – индуктивность, мкГн.

Подставляя численные значения в формулу, получают значение L.

Расчет количества витков по индуктивности

Зная D каркаса и L, рассчитывают количество витков в катушке, формула имеет вид:

w = 32*√(L*D),

где:

• L – индуктивность, мкГн;
• D – диаметр каркаса, мм.

Если в качестве исходных параметров берутся длина навитого в ряд проводника и его диаметр, то количество витков находят, используя формулу:

w = l/d,

где:

• l – длина намотки, мм;
• d – диаметр провода, мм.

Измерения диаметра провода проводят линейкой или штангенциркулем.

Расчёт индуктивности прямого провода

Собираясь найти L круглого прямого проводника, обращаются к приближённой формуле:

L = (μ0/2π)*l*( μe*ln(l/r) + 1/4* μi,

где:

• μ0 – магнитная постоянная;
• μe – относительная магнитная проницаемость (ОМП) среды (для вакуума – 1);
• μi – ОМП проводника;
• l – длина провода;
• r – радиус провода.

Формула справедлива для длинного проводника.

Расчёт однослойной намотки

Однослойные дроссели без сердечника легко и быстро можно рассчитать при помощи онлайн-калькулятора, в окно которого можно забить все известные характеристики, и программа выдаст значение L.

Вычисления проводятся и вручную, с использованием математического выражения. Оно имеет вид:

L = D2*n2/45D + 100*l,

где:

• D – диаметр катушки, см;
• l – длина намотанного провода, см;
• n – количество витков.

Формула подходит для вычислений L дросселей без ферритовых сердечников.

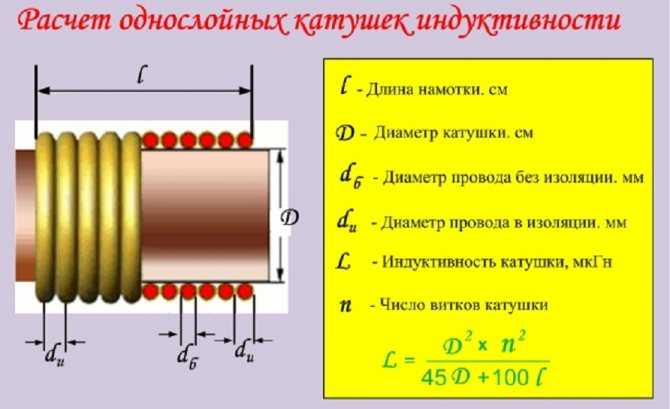
Однослойная катушка виток к витку

Дроссель с сердечником

При наличии сердечника следует учесть его размеры и форму. В случае одинаковых катушках индуктивность больше у той, которая располагается на сердечнике.

Расчёт однослойной намотки с сердечником

Многослойная намотка

Особенности расчёта при подобном способе наматывания провода заключаются в том, что нужно учитывать его толщину. Формула для дросселя без сердечника имеет вид:

N²=(L*(3Dk+9l+10t))/0.008Dk²,

где:

• Dk – общий диаметр (диаметр каркаса и намотки);
• t – толщина слоя;
• l – длина накрученного провода.

Все значения подставляют в мм, величину L – в мкГн.

Многослойная намотка

Схемы соединения катушек индуктивностей

Параллельное соединение индуктивностей

Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:

Последовательное соединение индуктивностей

Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:

Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.

Эквивалентная схема реальной катушки индуктивности

Каждый дроссель можно представить в виде эквивалентной схемы.

Данная схема состоит из элементов:

• Rw – сопротивление обмотки с выводами;
• L – индуктивность;
• Cw – паразитная ёмкость;
• Rl – сопротивление потерь.

Изготавливая индуктивный элемент, стремятся снизить величину сопротивления потерь, паразитную ёмкость. При работе катушки на низкой частоте учитывают сопротивление её обмотки Rw. На таких частотах действуют токи большой величины.

Эквивалентная схема дросселя

Правильно рассчитанная катушка индуктивности будет иметь высокую добротность (180-300) и стабильность работы при влиянии внешних условий (температуры и влажности). Зная способы различной намотки и манипуляции с шагом, можно уменьшить влияние паразитных факторов.

Индуктивность двухпроводной линии

Двухпроводная линия (рис. 1.16, а) состоит из двух параллельных проводов одинакового радиуса г, имеющих большую длину I по сравнению с расстоянием d между ними. Магнитная проницаемость материала проводов (г, окружающей среды — µ. Токи I в прямом и обратном проводах отличаются лишь направлением; начало координат взято в центре сечения левого провода.

Для отдельного провода ввиду его осевой симметрии, при пренебрежении искажением поля у его концов, применение закона полного тока к окружности радиуса дает:

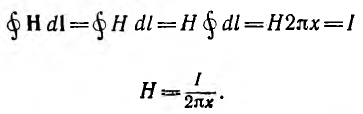
При интегрировании по окружности, лежащей внутри отдельного провода охватывается лишь часть L_Х всего тока, протекающая внутри круга радиуса х, равная при равномерном распределении тока по сечению

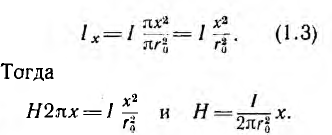
В воздухе между проводами на линии, соединяющей центры их сечений направления полей, создаваемых обоими токами согласно правилу правого винта, совпадают и напряженности поля и индукции складываются:

Эти же формулы справедливы и для т. е. снаружи линии, но здесь они дают разность полей.

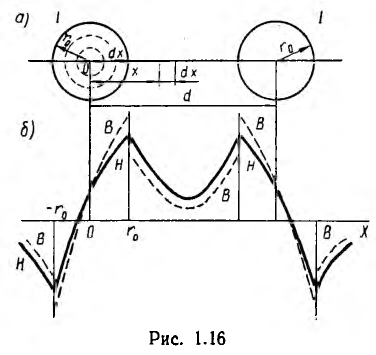
Внутри левого провода линии напряженность поля и индукция от обоих проводов будут:

Внутри правого провода соответственно,

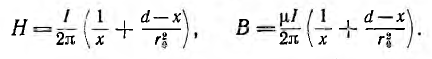
На рис. 1.16, б представлено распределение напряженности поля и индукции вдоль оси х для магнитной проницаемости материала проводов µ > µ. Посередине между проводами поле минимально, но в нуль не обращается. Поле также не равно нулю на осях проводов.

На внутренней стороне проводов напряженность поля и индукция больше, чем на внешней. В отличие от напряженности поля индукция имеет разрыв у поверхности проводов. Для вычисления индуктивности линии необходимо найти потокосцепление. Элементарный поток, проходящий через площадку Idx в воздухе между проводами,

Весь поток между проводами — внешний поток

одновременно является внешним потокосцеплением, так как сцепляется с контуром один раз. Поэтому

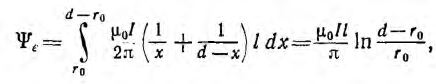
а соответствующая ему внешняя индуктивность

Для большинства линий расстояние d между проводами значительно превышает радиус r проводов. В этом случае

Для определения внутренней индуктивности, соответствующей внутреннему потоку, при d > r поле внутри провода линии может вычисляться как поле уединенного провода, так как поле, создаваемое вторым проводом внутри первого, по сравнению с полем первого, пренебрежимо мало. Тогда элементарный поток внутри провода

Так как поток dФ_i охватывает не весь ток, а только его часть , элементарное потокосцепление

Весь поток между проводами — внешний поток

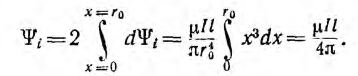
Соответственно, внутренняя индуктивность

Суммарная индуктивность линии

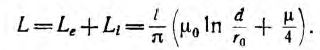
При медных или алюминиевых проводах () в большинстве случаев вторым членом можно пренебречь по сравнению с первым и тогда

Для стальных проводов () основной частью потока является
внутренний поток и индуктивность

практически не будет зависеть от расстояния между проводами.

Как выбрать ферритовый кольцевой сердечник?

Выбрать примерный размер ферритового кольца можно при помощи калькулятора для расчета импульсных трансформаторов и справочника по ферритовым магнитопроводам. И то и другое Вы можете найти в «Дополнительных материалах».

Вводим в форму калькулятора данные предполагаемого магнитопровода и данные, полученные в предыдущем параграфе, чтобы определить габаритную мощность срдечника.

Не стоит выбирать габариты кольца впритык к максимальной мощности нагрузки. Маленькие кольца мотать не так удобно, да и витков придётся мотать намного больше.

Если свободного места в корпусе будущей конструкции достаточно, то можно выбрать кольцо с заведомо бо’льшей габаритной мощностью.

импульсных источников питания на ферритовых кольцах https://www. ferrite. /user_files/File/. literature8.zip схема к статье:

Расчёт дросселя (статья) https://valvolodin. na. ms/drossel. html

Рассчет дросселей на резисторах МЛТ (прога) — https://rf. *****/s3/r-dros. html

Программа для расчёта высокочастотных трансформаторов и дросселей — https://www. /. gramm/5/3.shtml

Программа для расчёта импульсного трансформатора — https://www. /. gramm/5/2.shtml

Дроссели переменного тока радиоэлектронной аппаратуры — https://dmitriks. naro. ooks/dptra. djvu

Рассчёт дросселей и катушек книга — https://depositfiles. files/mcckejoig

Трансформаторы и дроссели 1.1 на archive. ***** —

Оптимальное проектирование силовых высокочастотных ферромагнитных устройств — https://dmitriks. naro. oks/opsvfu. djvu

«Импульсные источники вторичного электропитания в бытовой радиоаппаратуре» — https://dmitriks. naro. books1/iip. djvu

на 494 https://focus. /. 1d/slva001d. pdf

ТРАНСФОРМАТОРЫ И ДРОССЕЛИ ДЛЯ ИМПУЛЬСНЫХ ИСТОЧНИКОВ ПИТАНИЯ — https://members. kern. ouz/chokes. html https://www. /ser2800.cfm

Эквивалентная схема реальной катушки индуктивности

Каждый дроссель можно представить в виде эквивалентной схемы.

Данная схема состоит из элементов:

• Rw – сопротивление обмотки с выводами;
• L – индуктивность;
• Cw – паразитная ёмкость;
• Rl – сопротивление потерь.

Изготавливая индуктивный элемент, стремятся снизить величину сопротивления потерь, паразитную ёмкость. При работе катушки на низкой частоте учитывают сопротивление её обмотки Rw. На таких частотах действуют токи большой величины.

Правильно рассчитанная катушка индуктивности будет иметь высокую добротность (180-300) и стабильность работы при влиянии внешних условий (температуры и влажности). Зная способы различной намотки и манипуляции с шагом, можно уменьшить влияние паразитных факторов.

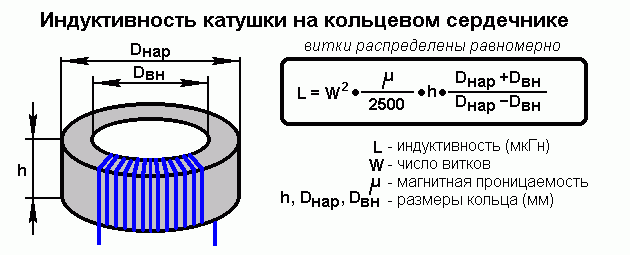
Индуктивность тороида и соленоида

Если на кольцевой сердечник — тороид, выполненный из материала проницаемостью µ > µ, нанести обмотку не по всей его длине (рис. 1.13), то только часть потока проходит по сердечнику, остальная часть — поток рассеяния — замыкается в воздухе. Тороид же, содержащий витки, плотно и равномерно распределенные по всей длине сердечника (рис. 1.14), замечателен тем, что практически весь магнитный поток сосредоточивается в сердечнике, т. е. потока рассеяния нет. Линии вектора напряженности поля представляют собой окружности, сцепляющиеся со всеми витками. Ввиду симметрии напряженность поля в каждой точке окружности по величине постоянна; по направлению она совпадает с касательной к окружности.

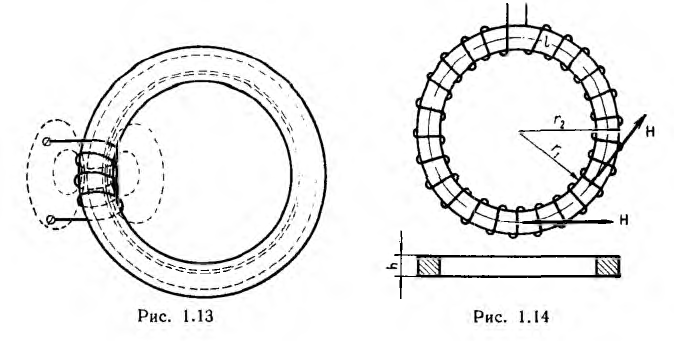
Тороиды широко применяются в трансформаторах, магнитных усилителях и электроизмерительных приборах.

Пусть тороид имеет прямоугольное сечение высотой Н, с радиусами г₁ и г₂, магнитная проницаемость материала µ.

По закону полного тока для окружности с радиусом

откуда

т. е. напряженность поля убывает по мере приближения к наружному краю тороида. Это в равной мере относится и к индукции

Поток в сердечнике тороида

а потокосцепление

Отсюда индуктивность тороида

Если расчет вести для средней линии I и приближенно считать поле в тороиде распределенным равномерно, то напряженность

где w — число витков на единицу длины, а магнитный поток и индуктивность, соответственно,

Обычно в реальных тороидах отношение что приводит при этих приближенных формулах к погрешности, не превышающей 1,2 %. Последняя формула для индуктивности может быть применена и к длинному соленоиду, рассматриваемому как часть тороида бесконечно большого радиуса. Для соленоида конечной длины µ=µ

где k

Как показывает точный расчет, этот коэффициент зависит от отношения диаметра D катушки к ее длине I (рис. 1.15). При = 0,1 коэффициент k — 0,96, поэтому при

Индуктивность кругового кольца круглого сечения

Теперь рассмотрим, какова будет индуктивность если провод свернуть в кольцо. Такой индуктивный элемент будет иметь вид

При этом его индуктивность можно вычислить по следующему выражению

для  постоянного тока

где R – радиус витка, м, R = D/2;

r – радиус провода, м, r = d/2;

μ – магнитная постоянная, μ = 4π•10-7 Гн/м.

Так же как и для проводника существует выражение для индуктивности кругового витка на любой частоте

где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Определяется также как и для прямого проводника.

Пример. В качестве примера рассчитаем индуктивность такого же провода, как и в первом примере, только свёрнутом в кольцо. В этом случае диаметр провода d = 2 мм, а диаметр кольца D = l/π = 4/3,142 ≈ 1,273 м, провод выполнен из меди (γ = 5,81*107 См/м).

Для постоянного тока индуктивность составит

На частоте 50 кГц

В следующей части я продолжу рассмотрение расчётов индуктивности для различных индуктивных элементов.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Что такое катушка индуктивности

Данный элемент ещё называют дросселем. Это свёрнутый в спираль изолированный провод. Для такой спирали характерны большие индуктивные и маленькие ёмкостные параметры.

Важно! Дроссель препятствует протеканию переменного тока, потому что обладает существенной инерционностью. Она препятствует любому изменению проходящего через витки тока

При этом нет разницы, увеличивается он или уменьшается.

В связи с этим данные элементы применяют в электротехнике для осуществления:

• токоограничения;
• ослабления биений;
• помехоподавления;
• формирования магнитного поля;
• изготовления датчиков движения.

Дроссель входит в систему колебательного контура в цепях резонанса и применяется в линиях задержки.

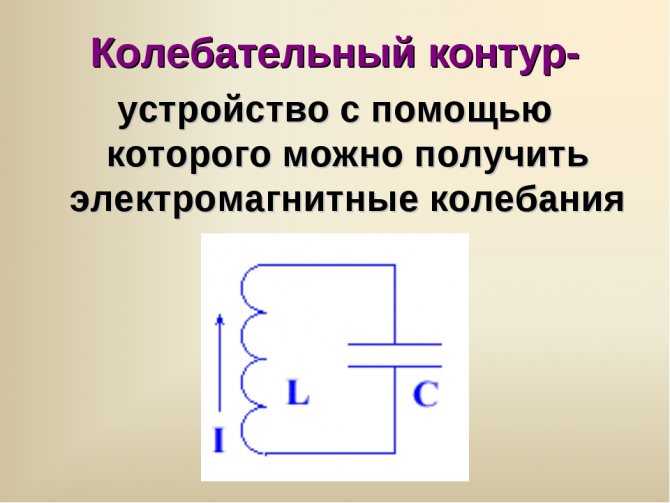
Применение L в колебательном контуре

Индуктивность и конденсатор

Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:

Ce = C : (1 – 4Π2f2LC),

где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.

Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.

Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:

Lk = Lp + Lm + Lb,

где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.

Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:

Lk = Lc : n + µ0 l х d : (3b) + Lb,

где l – длина шин, b – ее ширина, а d – расстояние между шинами.

Чтобы снизить индуктивность устройства, необходимо токоведущие части конденсатора расположить так, чтобы взаимно компенсировались их магнитные поля. Иными словами, токоведущие части с одинаковым движением тока нужно удалять друг от друга как можно дальше, а с противоположным направлением сближать. При совмещении токоотводов с уменьшением толщины диэлектрика можно снизить индуктивность секции. Этого можно достигнуть еще путем деления одной секции с большим объемом на несколько с более мелкой емкостью.

Общие сведения

Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.

Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.

Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.

Среди основных свойств индуктивности выделяются:

1. Величина параметра никогда не может быть меньше нуля.
2. Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.

Получение исходных данных для простого расчёта импульсного трансформатора.

Помню, когда наши электросети ещё не приватизировали иностранцы, я строил импульсный блок питания. Работы затянулись до ночи. Во время проведения последних испытаний, вдруг обнаружилось, что ключевые транзисторы начали сильно греться. Оказалось, что напряжение сети ночью подскочило аж до 256 Вольт!

Конечно, 256 Вольт, это перебор, но ориентироваться на ГОСТ-овские 220 +5% –10% тоже не стоит. Если выбрать за максимальное напряжение сети 220 Вольт +10%, то:

242 * 1,41 = 341,22V (считаем амплитудное значение).

341,22 – 0,8 * 2 ≈ 340V (вычитаем падение на выпрямителе).

Определяем примерную величину индукции по таблице.

Пример: М2000НМ – 0,39Тл.

Частота генерации преобразователя с самовозбуждением зависит от многих факторов, в том числе и от величины нагрузки. Если выберите 20-30 кГц, то вряд ли сильно ошибётесь.

Граничные частоты и величины индукции широко распространённых ферритов.

Граничная частота при tg δ ≤ 0,1, МГц

Магнитная индукция B при Hм = 800 А / м, Тл