Калькулятор для расчета катушки индуктивности

Магнитное поле

Это словосочетание знакомо нам со школьной скамьи. Но многие уже забыли о том, что оно означает. Хотя каждый из нас помнит, что магнитное поле способно воздействовать на предметы, притягивая или отталкивая их. Но, помимо этого, у него есть и другие особенности: например, магнитное поле может воздействовать на электрически заряженные объекты, а это значит, что электричество и магнетизм тесно связаны между собой, и одно явление может плавно перетекать в другое. Учёные поняли это достаточно давно и поэтому стали называть все эти процессы вместе одним словом — «электромагнитные явления». На самом деле электромагнетизм — довольно интересная и ещё не до конца изученная область физики. Она очень обширна, и те знания, что мы можем здесь изложить вам, — это очень малая часть того, что известно человечеству о магнетизме сегодня.

А сейчас перейдём непосредственно к предмету нашей статьи. Следующий раздел будет посвящён рассмотрению непосредственно устройства катушки индуктивности.

Методики расчета индуктивности катушек

Основным элементом катушек индуктивности является токовод. Величина индуктивности определяется конструкцией токовода и его размерами.

Полная индуктивность медного провода круглого сечения длиной lПР

и диаметромd равна

Из (3.1) следует, что индуктивность провода уменьшается с ростом его диаметра. Это свойство широко используют в УКВ аппаратуре для уменьшения индуктивности соединительных проводов за счет увеличения их диаметра.

Если одиночный проводник согнуть, например, в кольцо, то его индуктивность уменьшится из-за встречного направления токов в соседних частях кольца. Однако, для круглого кольца индуктивность будет наибольшей по сравнению с индуктивностью витка любой другой конфигурации, поскольку круглый виток охватывает наибольшую площадь, обеспечивая наибольшее потокосцепление.

Индуктивность круглого плоского витка диаметром D

из провода круглого сечения длинойlПР и диаметромdПР равна

При сворачивании проводника в несколько витков w

одинакового диаметра образуется катушка, индуктивность которой можно определить как суммарную индуктивность всех витков с учетом взаимоиндукцииM между ними:

Индексы при М

указывают на взаимную индуктивность между первым и вторым, вторым и третьим, первым и третьим витками и т.д. Если известен коэффициент связи, который определяется равенством

то индуктивность катушки с произвольным числом витков определяется из

Для сплошной намотки τ=d

Индуктивность многослойной катушки незначительно зависит от диаметра провода, так как определяется в основном взаимоиндукцией между витками.

Из-за трудности определения коэффициента связи выражение (3.5) обычно применяют для расчета катушек индуктивности с небольшим числом витков (обычно не более шести).

Для катушек с однородным замкнутым магнитопроводом (с тороидальным сердечником) выражение для определения индуктивности принимает вид

• где μ – начальная магнитная проницаемость сердечника (μ =1 для диэлектрического каркаса или воздуха);
• μ =4π·10-7Гн/м – магнитная постоянная;
• w – число витков обмотки;
• S — площадь поперечного сечения катушки;

Таким образом, увеличение индуктивности катушки может быть достигнуто за счет увеличения числа витков, магнитной проницаемости сердечника, площади поперечного сечения магнитопровода, а также уменьшения длины намотки.

В высокочастотных катушках замкнутый магнитопровод как правило отсутствует, поэтому индуктивность катушки будет меньше, рассчитанной по (3.7). Для учета рассеивания магнитного потока на краях катушки вводится поправочный коэффициент k

, который зависит от отношения диаметра катушки к длине намотки

Для практических расчетов однослойных цилиндрических катушек, намотанных виток к витку

(рис.3.2 а), используют выражение

1. μ – начальная магнитная проницаемость сердечника (μ =1 для катушек без магнитного сердечника);
2. μ =4π·10-7Гн/м – магнитная постоянная;
3. w – число витков обмотки;

D

– диаметр катушки;

Для практических расчетов однослойных цилиндрических катушек без сердечника, намотанных с принудительным шагомτ (рис.3.2 б), индуктивность рассчитывают по (3.9), но полученный результат уменьшают на поправкуΔL где τ

– шаг намотки;

L

– индуктивность катушки, определенная по (3.9) приμ =1.

Для практических расчетов индуктивности тороидальной однослойной катушки, намотанной сплошным слоем на круглом магнитном сердечнике прямоугольного сечения

(рис.3.2 в), используют выражение

• D – внешний диаметр сердечника тороида;
• d – внутренний диаметр сердечника тороида;
• h – высота сердечника тороида.

Для практических расчетов многослойных катушек без сердечника

(рис.3.2 г) используют выражение

1. гдеDCP – средний диаметр катушки;
2. t — толщина катушки;
3. l — длина катушки.

Для практических расчетов многослойных секционированных катушек без сердечника

(рис.3.2 д) используют выражение

где LC

– индуктивность одной секции катушки;

n

– число секций;

kCB

– коэффициент связи между смежными секциями, зависящий от отношения(рис.3.3);

b

– расстояние между секциями.

Для практических расчетов плоских круглых спиральных катушек

(рис.3.2 е) используют выражение

где DBH

,DH –внутренний и наружный диаметры катушки, соответственно.

Для практических расчетов плоских квадратных спиральных катушек

(рис.3.2 ж)используют выражение

где АBH

,АH –внутренняя и наружная стороны катушки, соответственно.

Практическое применение

Эти формулы имеют очень широкое применение ввиду повсеместного распространения катушек индуктивности. Как мы уже выяснили, бывают разные виды катушек, каждый из которых соответствует своему применению. В связи с этим становится необходимым как-то разделять их по характеристикам, ведь для каждой отрасли необходима своя определённая индуктивность и добротность.

В основном расчет индуктивности катушек применяется на производстве и в электротехнике. Каждый радиолюбитель должен знать, как производить расчет индуктивности, иначе как ему определить, какая катушка из огромного множества подойдёт для его цели, а какая — нет.

Выбираем магнитопровод

Вашему вниманию подборки материалов: Конструирование источников питания и преобразователей напряжения Разработка источников питания и преобразователей напряжения. Типовые схемы. Примеры готовых устройств. Онлайн расчет. Возможность задать вопрос авторам Практика проектирования электронных схем Искусство разработки устройств. Элементная база. Типовые схемы. Примеры готовых устройств. Подробные описания. Онлайн расчет. Возможность задать вопрос авторам

Если частота работы устройства до 3 кГц, то подойдет магнитопровод из трансформаторного железа. Если частота выше 7 кГц, то предпочтение следует отдать ферритам. На частотах 3 — 7 кГц можно использовать и железные и ферритовые сердечники. Но эффективность устройств на этих частотах обычно ниже, чем на других, так как тут железо уже теряет свою привлекательность, растут потери, а ферриты еще не могут раскрыть свой потенциал. До 150 кГц для дросселя с зазором (а подавляющее большинство дросселей делается с зазором), марка феррита значения не имеет. От магнитной проницаемости феррита в расчете ничего не зависит. На частотах свыше 150 кГц следует применять специальные высокочастотные марки ферритов.

Расчет для железа и ферритов на разных частотах имеет только одно отличие. Для железа максимальная индукция выбирается в районе 1 Тл. Для ферритов: при частоте до 100 кГц — 0.3 Тл, при частоте выше 100 кГц — 0.1 Тл. При желании снизить потери на перемагничивание магнитопровода максимальная индукция выбирается еще меньше.

Провод выбирается, исходя из плотности тока 5А / 1 кв. мм сечения. Это хуже европейских стандартов, но, как показала практика, вполне приемлемо. Если сила тока небольшая (менее 0.25 А), то дроссель мотается одним проводом нужного диаметра, если более 0.25 А, то жгутом из проводов 0.25 мм (для исключения скин — эффекта). Один такой провод хорошо работает при токе до 0.25 А.

Проверяя, хватит ли места для обмотки в окне магнитопровода, мы полагаем, что плотность заполнения окна не превысит 50%. Плотнее уложить провод удается только на станке. Вручную получить лучшую плотность нам не удавалось никогда.

Варианты измерения

Индуктивность катушки в физике определяется путём выполнения вычислений. Однако эту величину можно не только рассчитать, но и измерить. Делается это при помощи прямого или косвенного метода.

Прямой метод

Для измерения индуктивности катушки этим методом необходимо использовать специальные мостовые или прямопоказывающие устройства. С их помощью можно получить максимально точные данные, которые помогут выбрать требуемую катушку для схемы.

Порядок проведения измерений включает в себя следующие этапы:

1. К прямопоказывающему приспособлению подключают катушку.
2. После этого постепенно изменяют диапазоны измерений. Это делается до тех пор, пока получаемый результат не будет находиться примерно в середине интервала.
3. Полученный результат фиксируют и высчитывают с учётом цены деления прибора, а также коэффициента, соответствующего положению переключателя.

Измерение выполняют путём проведения таких действий:

1. Включённый мостовой прибор подсоединяют к катушке, индуктивность которой необходимо определить.
2. Аналогично прямопоказывающему устройству проводят переключение интервалов измерений.
3. После каждого такого действия ручку регулятора балансировки моста поочерёдно перемещают в одно и другое предельное положение.
4. Как только удалось определить диапазон, в котором мост будет сбалансирован, можно выполнять дальнейшие действия.
5. На следующем этапе измерений выполняется постепенное перемещение стрелочного индикатора.
6. После того как в динамике прибора исчезнет звук, необходимо зафиксировать показатели.
7. Затем их рассчитывают в соответствии с ценой деления шкалы и предусмотренным коэффициентом.

Косвенное определение

Для того чтобы измерить коэффициент самоиндукции, необходимо провести несколько подготовительных мероприятий. В первую очередь нужно собрать измерительную цепь по стандартной схеме, а также подготовить все необходимые приспособления (генератор синусоидального напряжения, частотомер, а также миллиамперметр и вольтметр, рассчитанные на переменный ток).

Порядок определения параметра:

1. К выходу генератора параллельно подключают вольтметр. Он должен быть переключён в режим, при котором верхнее предельное значение будет соответствовать напряжению в 3−5 вольт.
2. Аналогично подсоединяют и частотомер.
3. Отдельно собирают вторую цепь. В ней последовательно соединяют миллиамперметр и катушку, индуктивность которой нужно определить.
4. Затем обе цепи подключают параллельно друг к другу.
5. Подключённый генератор устанавливают в режим выработки синусоидального напряжения.
6. Путём изменения частоты добиваются такой работы приборов, при которой вольтметр будет показывать примерно 2 вольта. При этом сила тока на миллиамперметре будет постепенно уменьшаться.
7. После этого ручку частотомера перемещают в положение, соответствующее частоте измерений.
8. Как только эти действия будут выполнены, можно фиксировать значения.

Векторная диаграмма реальной катушки и полное её сопротивление

Несовпадение по фазе слагаемых в выражении (13.12) затрудняет определение амплитуды и действующей величины приложенного к цепи напряжения U. Поэтому воспользуемся векторным способом сложения синусоидальных величин. Амплитуды составляющих общего напряжения

UmR = RIm;       UmL = ωLIm ,

а действующие величины

UR = RI; UL = XLI .

Вектор общего напряжения

U = UR + UL

Для того чтобы найти величину вектора U, построим векторную диаграмму (рис. 13.10, а), предварительно выбрав масштабы тока Mi и напряжения Мu.

За исходный вектор диаграммы принимаем вектор тока I. Направление этого вектора совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза заданного тока Ψi =0). Как и ранее, эту ось удобно (но не обязательно) направить по горизонтали.

Вектор UR по направлению совпадает с вектором тока I, а вектор UL направлен перпендикулярно вектору I с положительным углом.

Из диаграммы видно, что вектор тока I общего напряжения U отражает вектор тока I на угол φ>0, но φ<90°, а по величине равен гипотенузе прямоугольного треугольника, катетами которого являются векторы падений напряжения в активном и индуктивном сопротивлениях UR и UL :

UR = Ucosφ 

Проекция вектора напряжения U на направление вектора тока называется активной составляющей вектора напряжения и обозначается Ua. Для катушки по схеме рис. 13.9 при Ua = UR

U = Usinφ                                                        (13.14)

Проекция вектора напряжения U на направление, перпендикулярное вектору тока, называется реактивной составляющей вектора напряжения и обозначается Up. Для катушки Up = UL

При токе i = Imsinωt уравнение напряжения можно записать на основании векторной диаграммы в виде

U = Umsin(ωt+φ)

Стороны треугольника напряжений, выраженные в единицах напряжения, разделим на ток I. Получим подобный треугольник сопротивлений (рис. 13.10, б), катетами которого являются активное R = UR/I и индуктивное XL = UL/I, сопротивления, а гипотенузой величина Z = U/I.

Отношение действующего напряжения к действующему току данной цепи называется полным сопротивлением цепи. Стороны треугольника сопротивлений нельзя считать векторами, так как сопротивления не являются функциями времени. Из треугольника сопротивлений следует

Понятие о полном сопротивлении цепи Z позволяет выразить связь между действующими величинами напряжения и тока формулой, подобной формуле Ома:

Из треугольников сопротивления и напряжения определяются

cosφ = UR/U = R/Z;    sinφ = UL/U = XL/Z;    tgφ = UL/UR = XL/R. (13.18)

Конструкция катушки индуктивности

Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.

Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.

Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.

Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.

Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.

Индуктивность кругового кольца круглого сечения

Теперь рассмотрим, какова будет индуктивность если провод свернуть в кольцо. Такой индуктивный элемент будет иметь вид

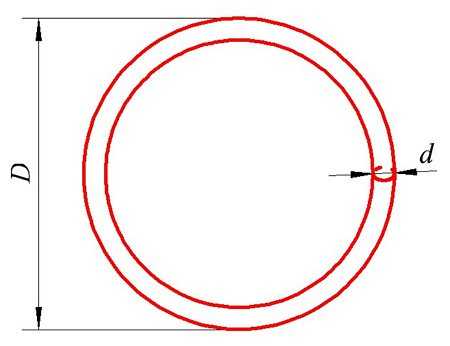
При этом его индуктивность можно вычислить по следующему выражению

для постоянного тока

где R – радиус витка, м, R = D/2;

r – радиус провода, м, r = d/2;

μ – магнитная постоянная, μ = 4π•10-7 Гн/м.

Так же как и для проводника существует выражение для индуктивности кругового витка на любой частоте

где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Определяется также как и для прямого проводника.

Пример. В качестве примера рассчитаем индуктивность такого же провода, как и в первом примере, только свёрнутом в кольцо. В этом случае диаметр провода d = 2 мм, а диаметр кольца D = l/π = 4/3,142 ≈ 1,273 м, провод выполнен из меди (γ = 5,81*107 См/м).

Для постоянного тока индуктивность составит

На частоте 50 кГц

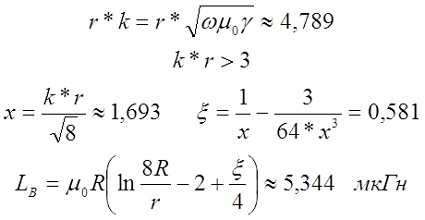
В следующей части я продолжу рассмотрение расчётов индуктивности для различных индуктивных элементов.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Что такое катушка индуктивности

Данный элемент ещё называют дросселем. Это свёрнутый в спираль изолированный провод. Для такой спирали характерны большие индуктивные и маленькие ёмкостные параметры.

Важно! Дроссель препятствует протеканию переменного тока, потому что обладает существенной инерционностью. Она препятствует любому изменению проходящего через витки тока. При этом нет разницы, увеличивается он или уменьшается

При этом нет разницы, увеличивается он или уменьшается.

В связи с этим данные элементы применяют в электротехнике для осуществления:

• токоограничения;
• ослабления биений;
• помехоподавления;
• формирования магнитного поля;
• изготовления датчиков движения.

Дроссель входит в систему колебательного контура в цепях резонанса и применяется в линиях задержки.

Применение L в колебательном контуре

Что такое катушка индуктивности

Данный элемент ещё называют дросселем. Это свёрнутый в спираль изолированный провод. Для такой спирали хаpaктерны большие индуктивные и маленькие ёмкостные параметры.

Важно! Дроссель препятствует протеканию переменного тока, потому что обладает существенной инерционностью. Она препятствует любому изменению проходящего через витки тока

При этом нет разницы, увеличивается он или уменьшается.

В связи с этим данные элементы применяют в электротехнике для осуществления:

• токоограничения;
• ослабления биений;
• помехоподавления;
• формирования магнитного поля;
• изготовления датчиков движения.

Дроссель входит в систему колебательного контура в цепях резонанса и применяется в линиях задержки.

Что такое катушка индуктивности

Данный элемент ещё называют дросселем. Это свёрнутый в спираль изолированный провод. Для такой спирали характерны большие индуктивные и маленькие ёмкостные параметры.

Важно! Дроссель препятствует протеканию переменного тока, потому что обладает существенной инерционностью. Она препятствует любому изменению проходящего через витки тока

При этом нет разницы, увеличивается он или уменьшается.

В связи с этим данные элементы применяют в электротехнике для осуществления:

• токоограничения;
• ослабления биений;
• помехоподавления;
• формирования магнитного поля;
• изготовления датчиков движения.

Дроссель входит в систему колебательного контура в цепях резонанса и применяется в линиях задержки.

Применение L в колебательном контуре

Что такое катушка индуктивности

Данный элемент ещё называют дросселем. Это свёрнутый в спираль изолированный провод. Для такой спирали характерны большие индуктивные и маленькие ёмкостные параметры.

Важно! Дроссель препятствует протеканию переменного тока, потому что обладает существенной инерционностью. Она препятствует любому изменению проходящего через витки тока

При этом нет разницы, увеличивается он или уменьшается.

В связи с этим данные элементы применяют в электротехнике для осуществления:

• токоограничения;
• ослабления биений;
• помехоподавления;
• формирования магнитного поля;
• изготовления датчиков движения.

Дроссель входит в систему колебательного контура в цепях резонанса и применяется в линиях задержки.

Применение L в колебательном контуре

Одновитковой контур и катушка

Индуктивность контура, представляющего виток провода, зависит от величины протекающего тока и магнитного потока, пронизывающего контур. Для индуктивности контура формула определяет параметр, соответственно, через поток и силу тока:

Ослабление магнитного потока из-за диамагнитных свойств окружающей среды снижает индуктивность.

Параметр для многовитковой катушки пропорционален квадрату количества витков, поскольку увеличивается не только магнитный поток от каждого витка, но и потокосцепление:

Для того чтобы рассчитать индуктивность катушки формула должна учитывать не только количество витков, но и тип намотки и геометрические размеры.

Гидравлическая модель

Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.

Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.

Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.

Что такое катушка индуктивности

Данный элемент ещё называют дросселем. Это свёрнутый в спираль изолированный провод. Для такой спирали характерны большие индуктивные и маленькие ёмкостные параметры.

Важно! Дроссель препятствует протеканию переменного тока, потому что обладает существенной инерционностью. Она препятствует любому изменению проходящего через витки тока

При этом нет разницы, увеличивается он или уменьшается.

В связи с этим данные элементы применяют в электротехнике для осуществления:

• токоограничения;
• ослабления биений;
• помехоподавления;
• формирования магнитного поля;
• изготовления датчиков движения.

Дроссель входит в систему колебательного контура в цепях резонанса и применяется в линиях задержки.

Применение L в колебательном контуре

Конструкция катушки

По конструктивному исполнению индуктивные элементы различаются:

• видом намотки: винтоспиральная, винтовая; кольцевая;
• количеством слоёв: однослойные или многослойные;
• типом изолированного провода: одножильный, многожильный;
• наличием каркаса: каркасные или бескаркасные (при небольшом количестве витков толстого провода);
• геометрией каркаса: прямоугольный, квадратный, тороидальный;
• наличием сердечника: ферритовый, из карбонильного железа, электротехнической стали, пермаллоевый (магнитомягкий сплав), металлический (латунный);
• геометрией сердечника: стержневой (разомкнутый), кольцо-образный или ш-образный (замкнутый);
• возможностью изменять L в узких интервалах (движение сердечника по отношению к обмотке).

Существуют плоские катушки, в печатном исполнении устанавливаемые на платах цифровых устройств.

К сведению. Намотка провода может быть как рядовой (витком к витку), так и в навал. Последний способ укладки провода снижает паразитную ёмкость.

Конструкция катушек

Какие параметры есть у катушки?

Катушка обладает несколькими физическими характеристиками, отражающими её качество и пригодность для той или иной работы. Одной из них является индуктивность. Она численно равна отношению потока магнитного поля, создаваемого катушкой, к величине этого тока. Индуктивность измеряется в Генри (Гн) и в большинстве случаев принимает значения от единиц микрогенри до десятков Генри.

Индуктивность является, пожалуй, самым важным параметром катушки. Поэтому неудивительно, что большинство людей даже не думают о том, что существуют другие величины, способные описывать поведение катушки и отражать её пригодность для того или иного применения.

При выборе катушки индуктивности профессионалы также обращают внимание на сопротивление потерь. Как можно понять из этого словосочетания, оно отражает величину потерь электроэнергии, происходящих вследствие паразитных эффектов, таких как, например, нагревание проводов, происходящее по закону Джоуля-Ленца

Нетрудно понять, что чем ниже это значение для катушки, тем она лучше.

Ещё один параметр, который необходимо учитывать, — добротность контура. Она тесно связана с предыдущим параметром и представляет собой отношение реактивного сопротивления к активному (сопротивлению потерь). Соответственно, чем выше добротность — тем лучше. Её повышение достигается за счёт выбора оптимального диаметра провода, материала и диаметра сердечника, числа обмоток.

Сейчас рассмотрим подробнее самый важный и наиболее волнующий нас параметр — индуктивность катушки.

Индуктивность кругового кольца круглого сечения

Теперь рассмотрим, какова будет индуктивность если провод свернуть в кольцо. Такой индуктивный элемент будет иметь вид

При этом его индуктивность можно вычислить по следующему выражению

для  постоянного тока

где R – радиус витка, м, R = D/2;

r – радиус провода, м, r = d/2;

μ – магнитная постоянная, μ = 4π•10-7 Гн/м.

Так же как и для проводника существует выражение для индуктивности кругового витка на любой частоте

где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Определяется также как и для прямого проводника.

Пример. В качестве примера рассчитаем индуктивность такого же провода, как и в первом примере, только свёрнутом в кольцо. В этом случае диаметр провода d = 2 мм, а диаметр кольца D = l/π = 4/3,142 ≈ 1,273 м, провод выполнен из меди (γ = 5,81*107 См/м).

Для постоянного тока индуктивность составит

На частоте 50 кГц

В следующей части я продолжу рассмотрение расчётов индуктивности для различных индуктивных элементов.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Калькулятор расчета катушки индуктивности

Индуктивность можно рассчитать самостоятельно или выполнить онлайн расчет с помощью специального калькулятора. Для автоматического расчета наиболее часто используется программа Coil32. Её можно бесплатно скопировать с одноименного сайта либо воспользоваться онлайн калькулятором. Пользоваться этой программой достаточно просто.

При работе с ней сначала нужно выбрать тип изделия (однослойная или многослойная, с ферритовым сердечником или без него, возможны другие варианты). Задав в калькуляторе расчет геометрических параметров, диаметр провода, число витков, свойства сердечника можно с помощью программы получить ожидаемую индуктивность изделия. Для получения необходимой величины можно в расчетах изменять число витков и диаметр провода.

Собранное изделие по рассчитанным параметрам можно проверить с помощью тестера на соответствие необходимым параметрам. Такой прибор называется LC тестер. Он измеряет индуктивность катушек и ёмкость конденсаторов. При отклонении полученных параметров от заданной величины можно увеличить либо уменьшить количество витков проволоки на изделии.

При желании можно выполнить самостоятельно расчет индуктивности катушки без сердечника или с ним. Единой формулы нет, они строго индивидуальны для каждого случая. В общем случае они прямо пропорциональны количеству витков и диаметру витков. Например, расчет однослойной цилиндрической обмотки выполняют по формуле:

Расчет индуктивности катушки с сердечником более сложен. С его добавлением значение индуктивность сильно возрастает. В расчетах в формулу добавляются параметры магнитных свойств сердечника. Ещё более сложными являются формулы расчёта многослойных катушек или катушек тороидальной формы. При редком или первичном использовании лучше всего воспользоваться специальными калькуляторами. Полученные расчеты можно проверить по формулам вручную. В любом случае после изготовления можно проверить параметры собранного изделия и при необходимости их изменить.

Расчет параметров катушки

Приходится при расчётах рассматривать разные варианты. Расчет индуктивности зависит от исходных данных и заданных конечных параметров.

Расчет L в зависимости от заданной конструкции

Если исходными параметрами являются: w, D каркаса и длина намотанного провода, то формула для расчёта имеет вид:

L = 0,01*D*w2/(l/D) + 0,46,

где:

• D – диаметр каркаса, см;
• w – число витков;
• l – длина намотки, см;
• L – индуктивность, мкГн.

Подставляя численные значения в формулу, получают значение L.

Расчет количества витков по индуктивности

Зная D каркаса и L, рассчитывают количество витков в катушке, формула имеет вид:

w = 32*√(L*D),

где:

• L – индуктивность, мкГн;
• D – диаметр каркаса, мм.

Если в качестве исходных параметров берутся длина навитого в ряд проводника и его диаметр, то количество витков находят, используя формулу:

w = l/d,

где:

• l – длина намотки, мм;
• d – диаметр провода, мм.

Измерения диаметра провода проводят линейкой или штангенциркулем.

Расчёт индуктивности прямого провода

Собираясь найти L круглого прямого проводника, обращаются к приближённой формуле:

L = (μ0/2π)*l*( μe*ln(l/r) + 1/4* μi,

где:

• μ0 – магнитная постоянная;
• μe – относительная магнитная проницаемость (ОМП) среды (для вакуума – 1);
• μi – ОМП проводника;
• l – длина провода;
• r – радиус провода.

Формула справедлива для длинного проводника.

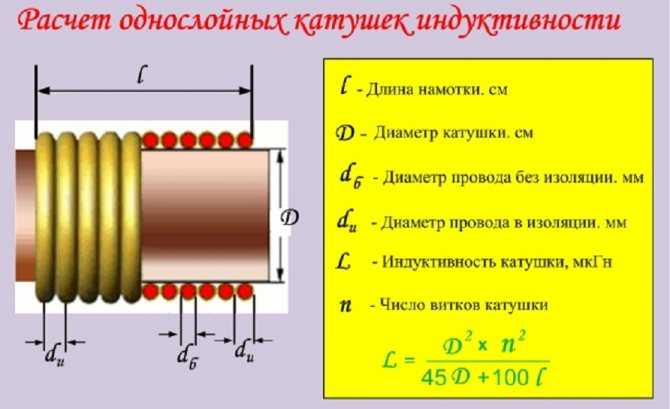
Расчёт однослойной намотки

Однослойные дроссели без сердечника легко и быстро можно рассчитать при помощи онлайн-калькулятора, в окно которого можно забить все известные характеристики, и программа выдаст значение L.

Вычисления проводятся и вручную, с использованием математического выражения. Оно имеет вид:

L = D2*n2/45D + 100*l,

где:

• D – диаметр катушки, см;
• l – длина намотанного провода, см;
• n – количество витков.

Формула подходит для вычислений L дросселей без ферритовых сердечников.

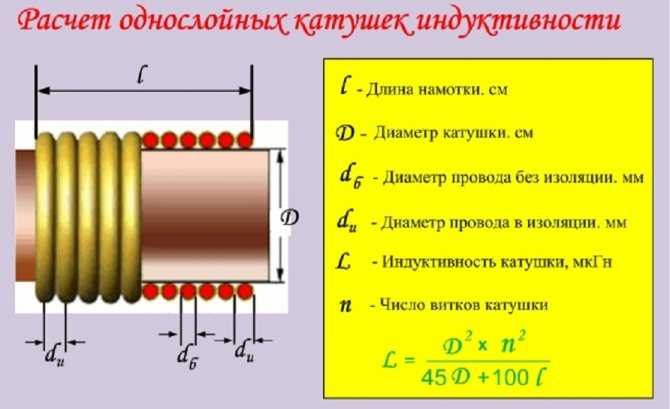
Однослойная катушка виток к витку

Дроссель с сердечником

При наличии сердечника следует учесть его размеры и форму. В случае одинаковых катушках индуктивность больше у той, которая располагается на сердечнике.

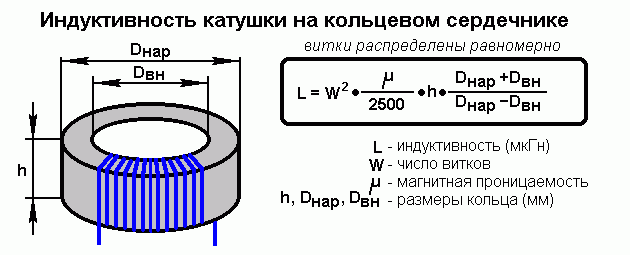
Расчёт однослойной намотки с сердечником

Многослойная намотка

Особенности расчёта при подобном способе наматывания провода заключаются в том, что нужно учитывать его толщину. Формула для дросселя без сердечника имеет вид:

N²=(L*(3Dk+9l+10t))/0.008Dk²,

где:

• Dk – общий диаметр (диаметр каркаса и намотки);
• t – толщина слоя;
• l – длина накрученного провода.

Все значения подставляют в мм, величину L – в мкГн.

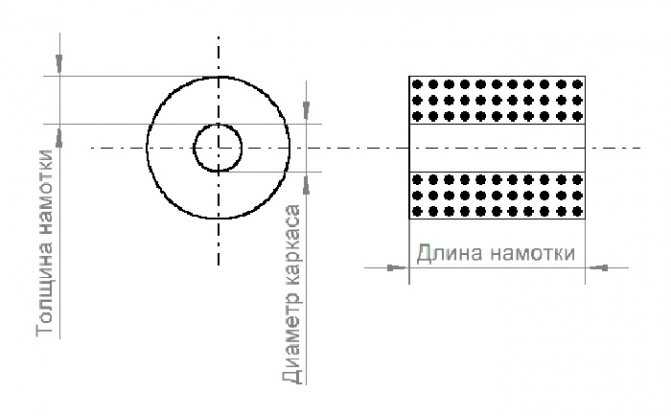
Многослойная намотка

Изготовление

Катушки индуктивности могут быть приобретены или изготовлены самостоятельно. Обычно приобретаются большие изделия. Наверное, никто не захочет самостоятельно наматывать дроссель для люминесцентной лампы. Небольшие обмотки для радиоэлектроники легко и с удовольствием изготавливаются своими руками. Навыки самостоятельного изготовления будут полезны при ремонте катушек или при изменении их рабочих параметров. Для увеличения их индуктивности используются специальные магнитные сердечники. Их изготавливают из смеси оксида железа с оксидами других металлов.

Воспользуйтесь другими онлайн калькуляторами:

Изолированная магнитная проволока наматывается непосредственно на магнитный сердечник, покрытый тонким слоем изолирующей бумаги. Перед изготовлением необходимо определить параметры с помощью специальных расчётных формул или программ. С их помощью будет определен размер и тип сердечника, число витков и диаметр проволоки.

Воспользуйтесь другими онлайн калькуляторами:

• Расчет веса электрического кабеля
• Онлайн расчет силы тока в цепи
• Перевод Ватт в Амперы
• Расчет потерь напряжения
• Онлайн расчет сечения кабеля

Расчет катушек на кольцах Amidon из порошкового железа:

Ферритовые кольца фирмы Amidon не имеют цветовой маркировки (блестящие черные либо тускло-серые), Здесь калькулятор для их расчета. Изделия из порошкового железа (карбонильного) маркируются цветом в зависимости от материала кольца. – здесь полный набор характеристик. Расчет ведется по формуле:

ВЫБЕРИТЕ КОЛЬЦО:

Тип материала кольца –	123678101215171826304052
Типоразмер кольца –	T-5T-10T-12T-16T-20T-25T-30T-37T-44T-50T-68T-80T-94T-106T-130

Доступная информация о кольце:

Цветовой код:  Материал:   Рабочие частоты LC цепей  Начальная магнитная проницаемость (μ):  Размеры (OD x ID x H):    дюймммA_L фактор:   мкГн/(N/100)2ВВЕДИТЕ ИСХОДНЫЕ ДАННЫЕ:

L

= мГнмкГннГн

– Требуемая индуктивность

Рассчитать

Результат:

N

=

– Число витков

МАТЕРИАЛ №0: В основном используется на частотах выше 100 МГц. Индуктивность (или число витков), полученная из расчетов, исходя из заданного параметра A_L, не может быть достаточно точной и сильно зависит от техники намотки.МАТЕРИАЛ №1: Очень похож на материал №3 за исключением более высокого объемного сопротивления и повышенной стабильности.МАТЕРИАЛ №2: Carbonyl ‘E’ порошковый материал с высоким объемным сопротивлением. Для изготовления высокодобротных катушек на частотах от 2 МГц до 20 МГц.МАТЕРИАЛ №3: Carbonyl ‘HP’ материал с прекрасной стабильностью и добротностью для низких частот от 50 КГц до 500 КГц.МАТЕРИАЛ №6: Carbonyl ‘SF’ материал. Предназначен для катушек с высокой добротностью и температурной стабильностью для частот 20 МГц — 50 МГц.МАТЕРИАЛ №7: Carbonyl ‘TH’ материал. Очень похож на №2 и №6, но имеет более высокую температурную стабильность.МАТЕРИАЛ №8: Этот материал имеет низкие потери в сердечнике и хорошую линейность в условиях высокого смещения по кривой намагничивания. Хороший высокочастотный материал. Самый дорогой материал.МАТЕРИАЛ №10: Порошковый материал «W». Обеспечивает хорошую добротность и высокую стабильность для частот от 40 МГц до 100 МГц.МАТЕРИАЛ №12: Синтетический оксидный материал, который обеспечивает хорошую добротность и умеренную стабильность для частот от 50 МГц до 200 МГц. Если высокое значение Q имеет первостепенное значение, этот материал является хорошим выбором. Если первостепенное значение имеет стабильность, предпочтительным будет материал № 17.МАТЕРИАЛ №15: Карбонильный материал «GS6». Обладает отличной стабильностью и хорошей добротностью. Хороший выбор для коммерческих частот вещания, где важны «Q» и стабильность.МАТЕРИАЛ №17: Это новый карбонильный материал, который очень похож на материал № 12, но он обладает лучшей температурной стабильностью. Однако по сравнению с материалом № 12 наблюдается небольшая потеря добротности, составляющая около 10% в диапазоне от 50 МГц до 100 МГц. На частотах выше 100 МГц добротность хуже примерно на 20%.МАТЕРИАЛ №18: Этот материал имеет низкие потери в сердечнике, аналогично материалу № 8, но с более высокой проницаемостью и более низкой стоимостью. Хорошие характеристики насыщения при постоянном токе.МАТЕРИАЛ №26: Материал с пониженным содержанием водорода. Обладает наивысшей проницаемостью из всех порошковых материалов. Используется для фильтров электромагнитных помех и дросселей постоянного тока.МАТЕРИАЛ №30: Хорошая линейность, низкая стоимость и относительно низкая проницаемость этого материала делают его популярным для мощных дросселей ИБП больших размеров.МАТЕРИАЛ №40: Недорогой материал. Имеет характеристики, похожие на очень популярный материал № 26. Хорошая линейность, низкая стоимость и относительно низкая проницаемость этого материала делают его популярным для мощных дросселей ИБП больших размеров.МАТЕРИАЛ №52: Этот материал имеет более низкие потери в сердечнике при высокой частоте и такую же проницаемость, что и материал № 26. Популярен для новых конструкций высокочастотных дросселей.

Ссылки по теме: